Tool Box Formulas
Roof slopes, stairs, frames, columns, and a myrid of carpentery problems are fodder for a formula. Quite often they are right angle problems, but circular stairs and decks can easily add circles and angles. It is a great advantage if you have a formula for a problem that's not readily solved by trial and error.
Let's take for example a large arch-top window that needs trim molding. Trial and error is not practical because the window is installed, is 30 ft. in the air, in the Great Room where all the lumber and tools are set up, But.... if I use a step stool to get to the top of the planer and I can step across to a ladder then I can sneak in there.
An arch is an arc, and an arc is a portion of the circumference of a circle, and I know that the diameter or radius of a circle is almost always important.
So I look in the Formula toolbox and- Viola!( or however that's spelled)- the
Formula for the radius of an arc or segment with known width and height
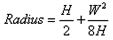
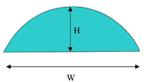 'x' is the height so 8 x 8 = 64"
'x' is the height so 8 x 8 = 64"
2304 divided by 64 = 36"
then the height 8" x 2 = 16"
so r = 36 + 16 = 52"
and with the radius I can draw the appropriate arc on a piece of plywod for a template or directly to a piece of wood.
 Pi = 3.14
Pi = 3.14
 D = 2 x R
D = 2 x R
diameter of a circle = PI * Radius
 C = pi*D
C = pi*D
Circumference of a circle = PI * Diameter
 A= pi x r squared
A= pi x r squared
Area of a circle = Pi * Radius squared
 Area of a Square = Side x Side
Area of a Square = Side x Side
 Area of a Rectangle = Length x Width
Area of a Rectangle = Length x Width
 Area of a Parellelogram = Base x Height
Area of a Parellelogram = Base x Height
 Volumn of a Cube = Length x Width X Height
Volumn of a Cube = Length x Width X Height
The following is a chart for figuring the chord lengths for a segmented frame.
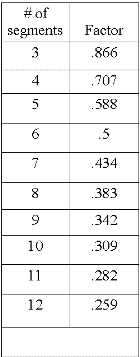
Diameter x factor = chord length. Let's say you would like to build a 8-sided frame and you want a 36" diameter inside. Using the chart take 36"*.383=3.06"(chord length).
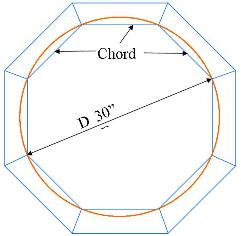
This gives you the ability to estimate material or rough cut to length.

Another interesting formula is determining the angle cuts of a segmented frame.
Let's use a four-sided frame as an example.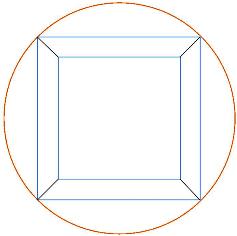 Assume that all frames are encompassed in a circle. A circle has 360 degrees. Divide 360 by thre number of corners on the frame and it gives you the angle degree the two corners will make when they are joined.
Assume that all frames are encompassed in a circle. A circle has 360 degrees. Divide 360 by thre number of corners on the frame and it gives you the angle degree the two corners will make when they are joined.
360/4=90 degrees.
To get the miter angle divide 90 by 2 and you get 45 degrees.
Another way is to divide 360 by the number of cuts you will make- in this case it will require 8 cuts to make the corners- 360/8=45.>br>
Let's do an 8-sided frame. An 8-sided frame has 8 corners and will require 16 cuts to miter those corners. 360/16=22.5 degrees.

Area of Triangle when the length of the three sides is known
1/4 * square-root [ P * (P-2a) * (P-2b) * (P-2c)] where P is total perimeter
and a, b and c are the lengths of the three sides

Area of a Sector of a Circle
Area=(m/360)*Pi*r^2 m= measurement of central angle
r= radius

Volume of sphere
4/3(pie)(r)3 pie=3.14
r=radius

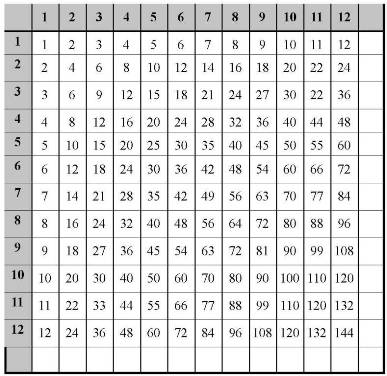
Multiplication Table
To Top of Page





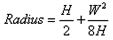
 'x' is the height so 8 x 8 = 64"
'x' is the height so 8 x 8 = 64"  Pi = 3.14
Pi = 3.14

 Assume that all frames are encompassed in a circle. A circle has 360 degrees. Divide 360 by thre number of corners on the frame and it gives you the angle degree the two corners will make when they are joined.
Assume that all frames are encompassed in a circle. A circle has 360 degrees. Divide 360 by thre number of corners on the frame and it gives you the angle degree the two corners will make when they are joined. 
