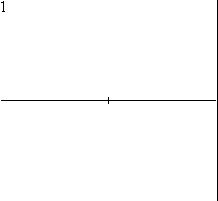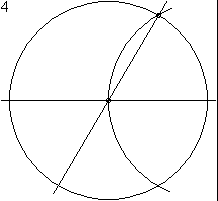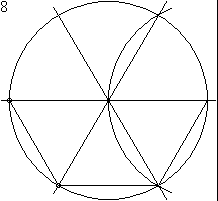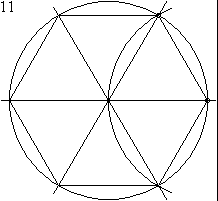Geometry- a tool for the carpenter

Geometry for the woodworker and the carpenter.

I use math nearly every day in my finish carpentry business.
In woodworking and cabinetry it's essential.
Along with all my other tools, I carry "cheat sheets" with various formulas with me. they are as important as any.

Any kind of carpentry work involves geometry
– it’s all about angles and levels and circles with their radii and diameters.
It's a HUGE advantage to be able to figure a diagonal measurement when doing layout work for a foundation, and it usually impresses other tradesmen if you have an accurate answer ready for a problem they can't solve by trial and error.
Geometry is extremely handy and I thought others would like to refresh some basic geometry skills also.

The images are from a Dover publication called the The cabinet-makers assistant originally published in 1853.

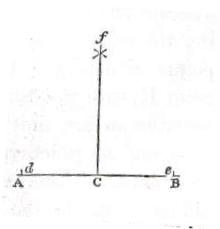
Problem 1 - At a given point on a straight line draw a line perpendicular to it.
Draw a line AB. Point C is equal distance from both ends. From C scribe an arc whose radius is greater than CA. Using the same radius scribe an arc from B in the same manner. Draw a straight line from c through the point of the intersection of the arcs.

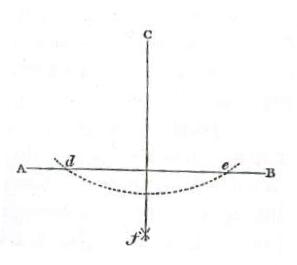
Problem 2 - From a given point let fall a straight line perpendicular upon a given line.
Let C be the given point and AB the given straight line.With C as center scribe an arc of any radius that will cut line AB at D and E. From D and E as centers and with a radius greater than half of DE scribe two arcs that intersect at F. Draw the perpendicular line DF.

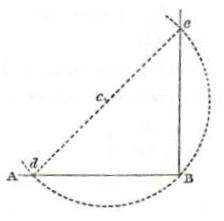
Problem 3 - From the extremity of a straight line draw a perpendicular line to it.
Let the straight line be AB and the extremity point be B. From any point C scribe an arc that is greater than a semicircle that will intersect the line at D and B. Through D and C draw a straight line to intersect the arc at E. Join E and B with a straight line.

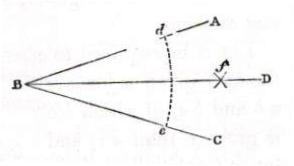
Problem 4- Bisect(divide into 2 equal parts)a given angle.
The given angle is ABC. From vertec B, with any radius BD scribe an arc DE to intersect the outsides of the given angle. From D and E as centers and with a radius greater than half of DE scribe two arcs to intersect at F. A straight line drawn from B through F will bisect the given angle.

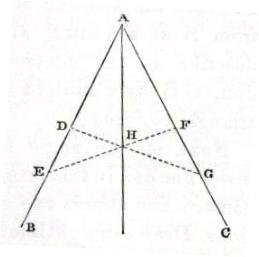
This problem may also be solved by rectilineal contruction using a ruler;
BAC is the given angle. On side AB make two points D and E. On side AC make AF equal to AD and Make AG equal to AE. Joine DG and EF with straight lines. They intersect at H. A straight line drawn from A through H will bisect the given angle.

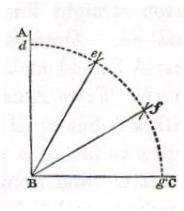
Problem 5 - Divide a right angle into 3 equal parts.
ABC is to be the right angle. From vertex B scribe an arc with any radius to intersect the right angle sides at D and G forming arc DG. Using the same radius scribe an arc from D intersecting DG at F and from G an arc intersecting at E. Straight lines from B throught E anf F will trisect the angle ABC.

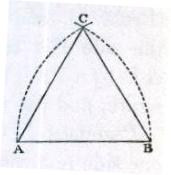
Problem 6 -Construct an equilateral tringle on a given straight line.
AB is the given base line. From the ends of the line and using points A and B as centers scribe an arc using AB as the radius scribe arcs intersecting at C. Straight lines from A to A and B to C will form an equilateral triangle.

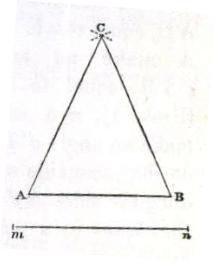
Problem 7 - Construct an isosceles triangle from a given base line.
AB is the given base line and MN is to be equal to the other two sides of the triangle. Using MN as the radius scribe arcs from points A and B to intersect at C. Draw lines from A and B to C.

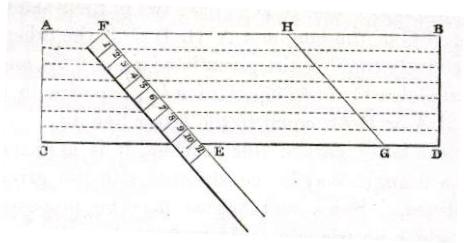
Problem 8 - Divide a board into equal rips.
Let the board be ABCD and the parallel sides be AB and CD,and whose width is 9".
DIvide it into 7 rips. Lay a rule diagonally acros the board. 7 inches will not extend across the board but if half of 7, or 3 1/2 is as added, then 10 1/2 wiil extend diagonally. This dimension can be dived into 1 1/2" along EF and then along HG.
Lines drawn through these marks will be equidistand and parallel.

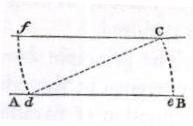
Problem 9 - Through a given point draw a line parallel to a given line AB.
From point C, the given point at a required distance fron AB, draw a line meeting AB at a point D.
From D, with the radius DC, scribe an arc meeting AB at E.
From C as the center with the same radius Scribe an arc DF.
At d scribe an arc to F with the radius of CE,
Through C anf F draw a straight line that is parallel to AB.

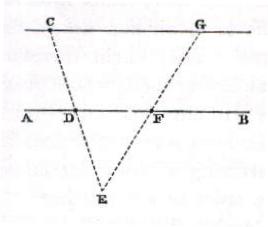
Problem 10 - Draw a line parallel to AB with a given point C at the required distance to AB by rectilineal construction.

From C draw a straight line to intersect AB at any point D and extend it until DE equals DC.
From E draw a straight line to intersect AB to F and extend this line to G until FG equals EF.
Through C and G draw a line that will be parallel to AB.

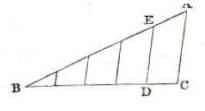
Problem 11 - Divide a line into any number of equal parts.

BC is the given line and divide it into 5 equal parts.
From the extremity of B, draw a line BA, forming any acute angle with BC. On BA measure 5 equal parts from B to A. Connect AC with a straight line.
From each of the other points on BA draw parallel lines to BC. This will divide BC into equal parts.

Problem 12 - Creating a regular hexagon with a ruler and compass

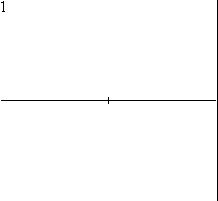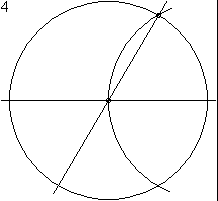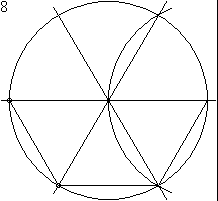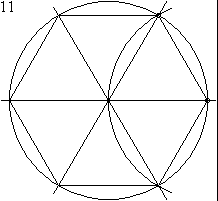
Problem 13 - Construction of a regular pentagon with a ruler and compass

From Geometry to Woodworking tips
From Geometry to American Architecture